Microscope Objective
If you have a close look at the objectives on your microscope, you’ll see a variety of information and numbers engraved on the barrel. As well as the magnification and the optical correction, you will see another number which has no units. This is the Numerical Aperture (or ‘NA’) of the objective (s. Figure 1).
The NA of an objective is an important aspect and relates to the image resolution. In brief, the resolution is the ability of the objective to distinguish details in your specimen. Without a correspondingly high NA, an objective with a high magnification would be unable to resolve sample detail.
In simple terms, the NA of a microscope objective is the ability of the lens to gather light at a fixed distance from the object on view. As light passes through a specimen, it enters the objective as an inverted cone. However, some of the light from the specimen is refracted (and reflected), but objectives with a high NA value permit increasingly oblique light waves to be gathered by the front lens which in turn will produce an image which is highly resolved and contains more detail and information than objectives which have lower NA.
Angular Aperture
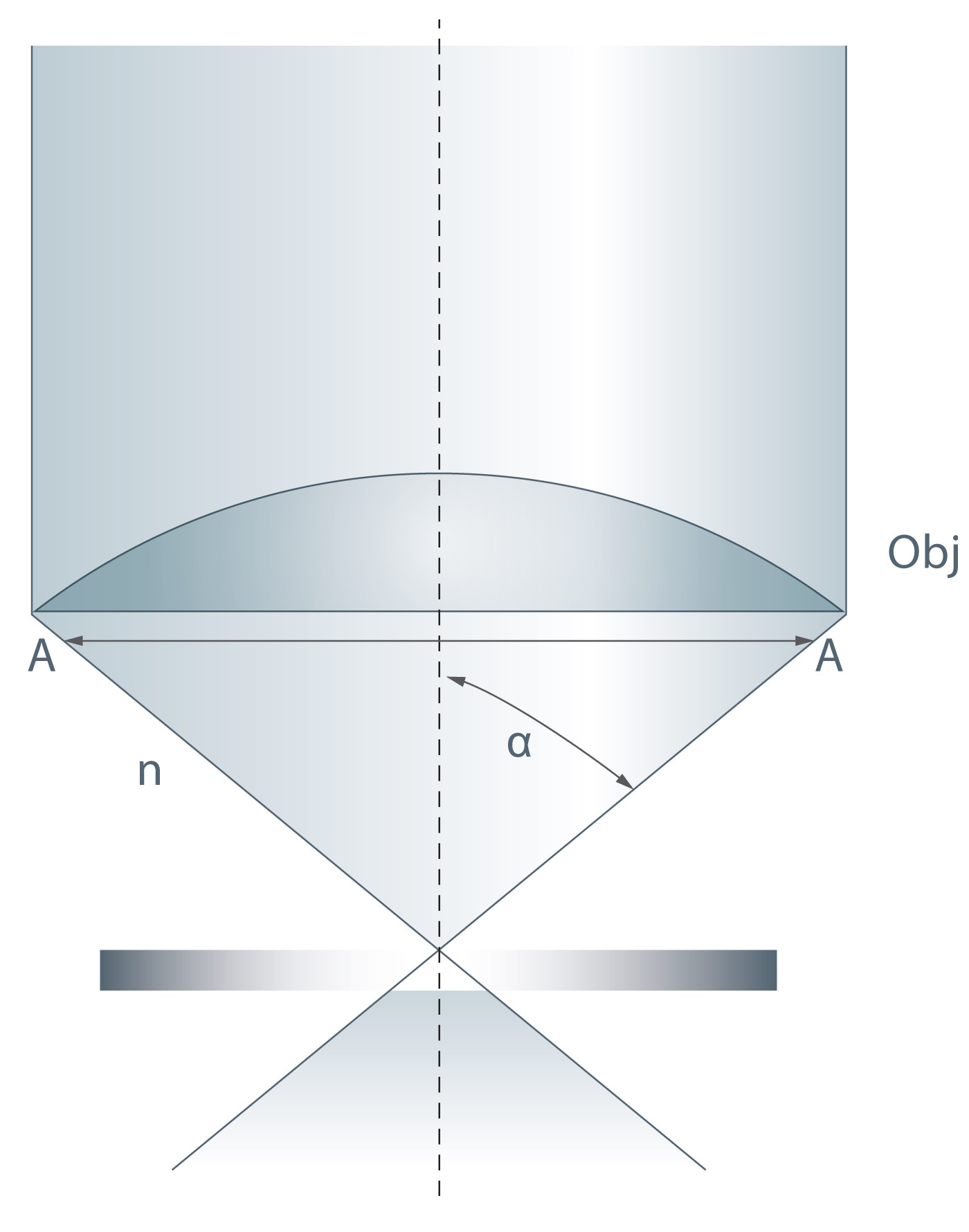
The maximum longitudinal angle of the cone of light collected by the front lens of the objective is known as the ‘angular aperture’ (s. Figure 1). In addition to an increasing NA, image brightness is also proportional to the angular aperture. The angular aperture, which varies with the objective focal length, relates to the maximum angle of image-forming light rays emanating from the specimen that the objective front lens can capture when the specimen is focused.
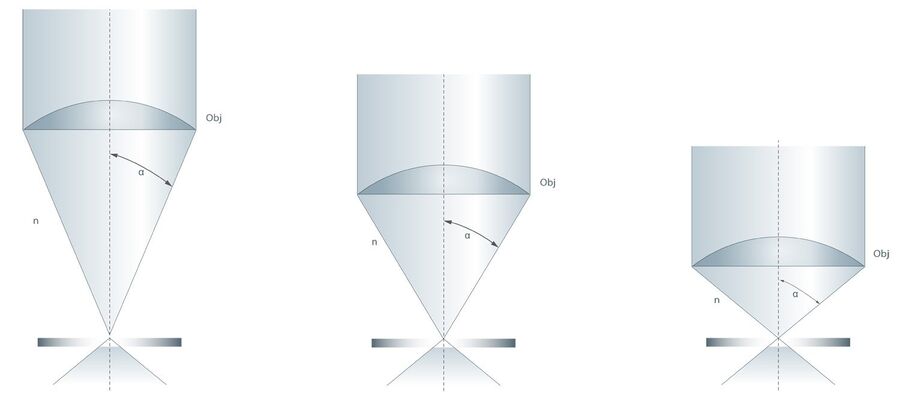
The angular aperture is inversely proportional to the focal length of the objective. As focal length decreases, there is an increase in the amount of light which the objective front lens can gather. In other words, if the objective is very close to the specimen, then more oblique light rays can be collected by the objective lens. It should be said that the angular aperture is usually determined by the optics within the objective and each objective lens will have an optimal focal length. Metaphorically, think of it this way: if you are standing in front of a door with a key hole which leads into another room, then when you are at a distance, you will only be able to see a little of the light and objects within the room. If you press your eye against the key hole, you will then see more of the detail and light in the room as you have, in theory, increased the angular aperture of your eye.
The image brightness and the image detail (resolution) which is collected and formed by an objective lens are related to the angular aperture. The light from the specimen continues through the air between the cover glass and the objective front lens or through an immersion medium.
Calculating NA
The numerical aperture can be expressed and determined by the following formula:
Numerical Aperture (NA) = n • sin(α)
In the above equation, ‘n’ is the refractive index of the medium between the cover glass and the front lens of the objective (for example; air, water or oil). The ‘α’ symbol relates to half of the angle of the cone of light which can be collected by the lens (i.e., the angular aperture; s. Figure 2).
Air has a refractive index which is approximately 1.0, whereas the refractive index of water is 1.3 and some immersion oils used for optical microscopy have a refractive index as high as 1.52.
Refraction
In order to fully understand NA, it is helpful to have an understanding of refraction. In optics and microscopy, refraction is a change in the direction of light waves passing through and coming from a specimen which is due to a change in the medium though which the light passes, be it air, glass, water or oil. Refraction is described in a formula known as ‘Snell’s Law’. Willebrord Snellius (1580-1626) was a Dutch mathematician and astronomer. As well as determining a new method of calculating the radius of the earth, he was also credited for mathematically describing refraction. However, he wasn’t the first to do so and it is more accurate to say that he ‘rediscovered’ diffraction as this had been described many centuries before by a Persian mathematician and physicist called Ibn Sahl. In his manuscript from 984, he described how curved lenses and mirrors bent and focused light.
Snell’s Law states that the ratio of the angles of incident and refracted light are equivalent to the reciprocal of the ratio of the refractive indices through which the light passes.
In simpler terms, when light travels from one medium to another it changes speed- for example, when passing from air to water, light slows down. In addition, the change in speed results in change in direction for light which enters a medium at an angle other than 90°. It should be noted that the frequency of light doesn’t change, but the wavelength will be determined by nature of the medium.
In theory, the maximum angular aperture of the light cone collected by the objective front lens would be 180°, which would give an α value of 90°. As the sine of 90 is one, this would mean that the theoretical NA of an objective which was able to collect 180° of the resultant light from a specimen in a medium of air would also be one. Clearly, the refractive index is the limiting factor in achieving the highest NA of an objective. Consequently, the high-NA objectives are those which use an immersion medium in place of air, such as oil or water. In reality, an NA of one with air between the specimen and the objective front lens is unachievable and therefore the highest NA of a ‘dry lens’ (i.e. a non-immersion objective) and is closer to 0.95. This is due to the fact that most lenses would not be able to collect 180° of light from the specimen and the widest angle is approximately 144°. The sine of 144° is 0.95 and as air has a refractive index of 1.0, the theoretical maximum NA is close to 0.95.
A high magnification objective lens with low NA will consequently have low resolution. Many microscopy companies offer objectives with as high an NA as possible. So, if you are in the position of buying new lenses for your microscope, you should always consider buying those objectives which offer the greatest NA within your budget.