Resolution and numerical aperture
The numerical aperture (NA) is related to the refractive index (n) of a medium through which light passes as well as the angular aperture (α) of a given objective (NA = n sinα). The resolution of an optical microscope is not solely dependent on the NA of an objective, but the NA of the whole system, taking into account the NA of the microscope condenser. More image detail will be resolved in a microscope system in which all of the optical components are correctly aligned, have a relatively high NA value and are working harmoniously with each other. Resolution is also related to the wavelength of light which is used to image a specimen; light of shorter wavelengths are capable of resolving greater detail than longer wavelengths.
There are 3 mathematical concepts which need to be taken into consideration when dealing with resolution: Abbe’s diffraction limit, Airy discs, and the Rayleigh criterion. Each of these are covered below in chronological order.
George Biddell Airy and ‘Airy Discs’ (1835)
George Biddell Airy (1801-1892) was an English mathematician and astronomer. By the 1826 (aged 25) he was appointed professor of mathematics at Trinity College and two years later, he was appointed professor of astronomy at the new Cambridge Observatory. From 1835 to 1881 he was the ‘Astronomer Royal’ and even has a lunar and Martian crater named in his honor.
Also in the year 1835, he published a paper in the Transactions of the Cambridge Philosophical Society entitled ‘On the Diffraction of an Object-Glass with Circular Aperture’ [1]. Airy wrote this paper very much from the view of an astronomer and in it he describes “the form and brightness of the rings or rays surrounding the image of a star as seen in a good telescope”. Despite writing in a different scientific field, these observations are relevant to other optical systems including microscopes.
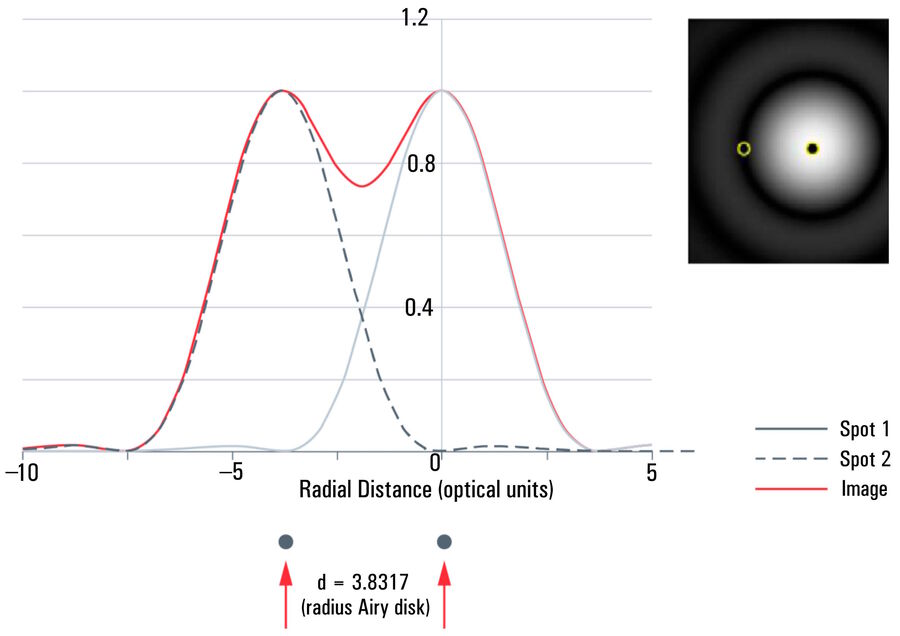
An Airy disc is the optimally focused point of light which can be determined by a circular aperture in a perfectly aligned system limited by diffraction. Viewed from above (Figure 1), this appears as a bright point of light around which are concentric rings or ripples (more correctly known as an Airy Pattern).
The diffraction pattern is determined by the wavelength of light and the size of the aperture through which the light passes. The central point of the Airy disc contains approximately 84% of the luminous intensity with the remaining 16% in the diffraction pattern around this point. There are of course many points of light in a specimen as viewed with a microscope, and it is more appropriate to think in terms of numerous Airy patterns as opposed to a single point of light as described by the term ‘Airy disc’.
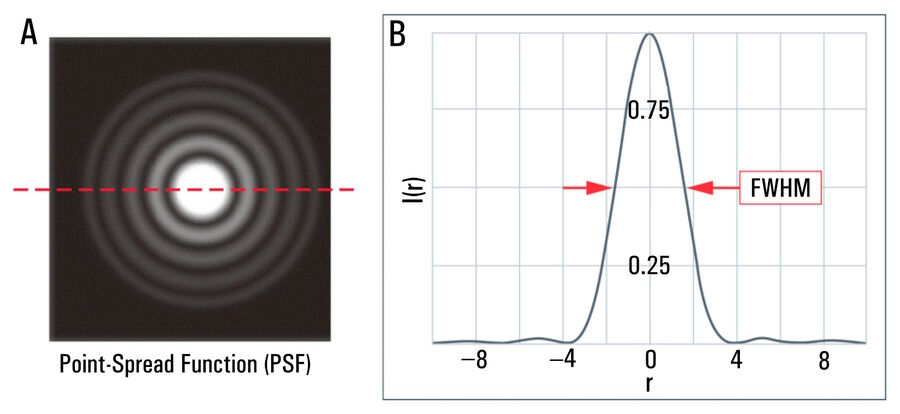
The three-dimensional (3D) representation of the Airy pattern, as illustrated in the right half of Figure 1, is also known as the ‘point-spread function’ (PSF) of an optical instrument which has no appreciable aberration.
Ernst Abbe and ‘Abbe’s Diffraction Limit’ (1873)
Ernst Karl Abbe (1840-1905) was a German mathematician and physicist. In 1866 he met Carl Zeiss and together they founded what was known as the ‘Zeiss Optical Works’, now known as Zeiss. In addition, he also co-founded Schott Glassworks in 1884. Abbe was also the first person to define the term numerical aperture. In 1873, Abbe published his theory and formula which explained the diffraction limits of the microscope [2]. Abbe recognized that specimen images are composed of a multitude of overlapping, multi-intensity, diffraction-limited points (or Airy discs).
In order to increase the resolution, d = λ/(2NA), the specimen must be viewed using either a shorter wavelength (λ) of light or through an imaging medium with a relatively high refractive index or with optical components which have a high NA (or, indeed, a combination of all of these factors).
However, even taking all of these factors into consideration, the possibilities with a real microscope are still somewhat limited due to the complexity of the whole system, transmission characteristics of glass at wavelengths below 400 nm, and the challenge to achieve a high NA in the complete microscope system. Lateral resolution in an ideal optical microscope is limited to around 200 nm, whereas axial resolution is around 500 nm (examples of resolution limits are given below).
John William Strutt and ‘The Rayleigh Criterion’ (1896)
John William Strutt, 3rd Baron Rayleigh (1842-1919) was an English physicist and a prolific author. During his lifetime, he wrote an astonishing 466 publications including 430 scientific papers. He wrote on a huge range of topics as diverse as bird flight, psychical research, acoustics and in 1895, he discovered argon (Ar) for which he was later awarded the Nobel prize for physics in 1904.
Rayleigh built upon and expanded the work of George Airy and invented the theory of the ‘Rayleigh criterion’ in 1896 [3]. The Rayleigh criterion defines the limit of resolution in a diffraction-limited system, in other words, when two points of light are distinguishable or resolved from each other.
Using the theory of Airy discs, if the diffraction patterns from two single Airy discs do not overlap, then they are easily distinguishable, ‘well resolved’ and are said to meet the Rayleigh criterion. When the center of one Airy disc is directly overlapped by the first minimum of the diffraction pattern of another, they can be considered to be ‘just resolved’ and still distinguishable as two separate points of light (Figure 2, mid). If the Airy discs are closer than this, then they do not meet the Rayleigh criterion and are ‘not resolved’ as two distinct points of light.
Full Width at Half Maximum (FWHM)
A more practical approach for resolution is the full width at half maximum (FWHM) intensity of an optically unresolved structure [4,5]. This value is relatively easy to measure with a microscope and has become a generally accepted parameter for comparison purposes. The theoretical value for the FWHM is RFWHM = 0.51λ/(NA) which is approximately λ/(2NA). So the FWHM as a resolution parameter is very close to Abbe’s diffraction limit, but also can be measured from microscope image data. For calibration or resolution-limit measurements, often beads or colloids of various diameters are imaged and measured.
These theoretical resolution values, derived from physical and mathematical assumptions, are estimates. They assume perfect imaging systems and a point light source in a vacuum or a completely homogeneous material as the sample or specimen. Of course, this assumption is almost never the case in real life, as many samples or specimens are heterogeneous. Because there is only a finite amount of light transmitting through the sample or reflecting from its surface, the measurable resolution depends significantly on the signal-to-noise ratio (SNR).
How to calculate the resolution of a microscope
Taking all of the above theories into consideration, it is clear that there are a number of factors to consider when calculating the theoretical limits of resolution. Resolution is also dependent on the nature of the sample. Let’s look at calculating resolution using the Abbe diffraction limit, Rayleigh Criterion, and also FWHM.
Firstly, it should be remembered that:
NA = n(sinα)
where n is the refractive index of the imaging medium and α is half of the angular aperture of the objective. The maximum angular aperture of an objective is around 144º. The sine of half of this angle is 0.95. If using an immersion objective with oil which has a refractive index of 1.52, the maximum NA of the objective will be 1.45. If using a ‘dry’ (non-immersion) objective the maximum NA of the objective will be 0.95 (as air has a refractive index of 1.0).
Abbe’s diffraction formula for lateral (XY) resolution is:
d = λ/(2NA)
where λ is the wavelength of light used to image a specimen. If using a green light of 514 nm and an oil-immersion objective with an NA of 1.45, then the (theoretical) limit of resolution will be 177 nm.
Abbe’s diffraction formula for axial (Z) resolution is:
d = 2λ/(NA)2
and again, if we assume a wavelength of 514 nm to observe a specimen with an objective having an NA value of 1.45, then the axial resolution will be 488 nm.
The Rayleigh Criterion is a slightly refined formula based on Abbe’s diffraction limits:
R = 1.22λ/(NAobj + NAcond)
where λ is the wavelength of light used to image a specimen. NAobj is the NA of the objective. NAcond is the NA of the condenser. The value ‘1.22’ is a constant. This is derived from Rayleigh’s work on Bessel Functions. These are used for calculating problems in systems such as wave propagation.
Taking the NA of the condenser into consideration, air (with a refractive index of 1.0) is generally the imaging medium between the condenser and the slide. Assuming the condenser has an angular aperture of 144º then the NAcond value will equal 0.95.
If using a green light of 514 nm, an oil-immersion objective with an NA of 1.45, condenser with an NA of 0.95, then the (theoretical) limit of resolution will be 261 nm.
As already mentioned, the FWHM can be measured directly from the PSF or calculated using:
RFWHM = 0.51λ/(NA).
Again using a light wavelength of 514 nm and an objective with an NA of 1.45, then theoretical resolution will be 181 nm. This value is very close to the lateral resolution calculated just above from the Abbe diffraction limit.
As stated above, the shorter the wavelength of light used to image a specimen, then the more the fine details are resolved. So, if using the shortest wavelength of visible light, 400 nm, with an oil-immersion objective having an NA of 1.45 and a condenser with an NA of 0.95, then R would equal 203 nm.
To achieve the maximum theoretical resolution of a microscope system, each of the optical components should be of the highest NA available (taking into consideration the angular aperture). In addition, using a shorter wavelength of light to view the specimen will increase the resolution. Finally, the whole microscope system should be correctly aligned.