Introduction
First, we shall give a brief description of the photomultiplier tube (PMT). Having established how light is converted into an electric signal, we shall go on to deal with different methods of primarily picking up this electric signal with the sensor. Basically, these methods apply equally to all sensors, although the suitability of the conversion techniques varies from sensor to sensor.
Finally, we describe the two recent sensor techniques deploying semiconductor technology (at least in part): the avalanche photo diode, APD and the hybrid detector, HyD.
The photomultiplier tube
This classic technology utilizes the outer photoelectric effect, which we shall first describe in brief. It will then be easy to understand why different materials are used for different purposes. Gain is produced by generating secondary electrons which are then amplified again in several stages. The amplification takes place at the so-called dynodes. Finally, the many electrons that have been created have to be discharged into the outer world. This job is done by the anode.
Turning photons into electrons (cathode)
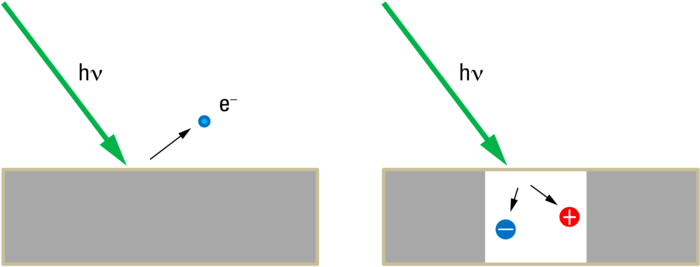
The outer photoelectric effect describes the observation that free electrons are generated at (initially metal) surfaces when light shines on them. The first photoelectric effect to be observed was the "Bequerel effect", where an electric potential can be seen at electrodes in conductive liquids when these electrodes are irradiated with light of different intensity [1]. This effect, similar to the effect seen with semiconductors, is usually called the "photovoltaic effect" nowadays and is the reason for the booming solar panel business on house roofs. Free electrons are not generated in this technology, which is why it is called an "inner photoelectric effect". This inner photoelectric effect is important for the avalanche photo diodes described in Chapter "The avalanche photodiode".
The outer photoelectric effect was observed and described by Heinrich Hertz [2], who determined a promotive impact of UV light on the generation of his spark gaps ("Tele-Funken"). Wilhelm Hallwachs [3] continued the studies on light-induced electricity, which explains why the outer photoelectric effect was called Hallwachs effect for a while. The measured phenomena were understood and interpreted by Albert Einstein [4]. By reviving the corpuscular theory of light by Newton [5] he was able to explain all the observations that could not be derived from wave theory.
Measuring the number of electrons released upon irradiation of one electrode (i.e. the current that can be detected via the second electrode), we find that this number is dependent on the intensity of the light. This is compatible with wave theory: the greater the field strength, the more energy is available for releasing the electrons. Examining the amount of kinetic energy of these electrons (the "starting speed"), however, we notice that this speed does not depend on the intensity, but on the wavelength only. Moreover, there is a maximum wavelength beyond which no more electrons are released. This maximum wavelength is a property of the cathode material. This contradicts the idea in wave theory that if we only add enough energy – just a bit longer for weak intensities – we can excite the receiver to release electrons.
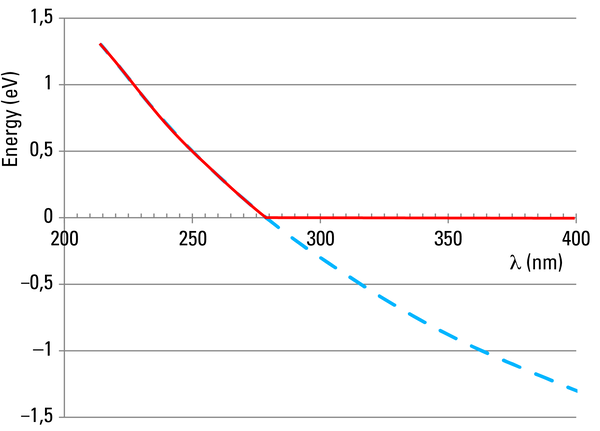
This behavior is explained by understanding photons as particles of light: after Max Planck had already introduced the "quantum of action" in 1900 to be able to describe the correct relationship between temperature and radiation energy [6], Einstein transferred this quantization to light energy itself. Light is thus divided up into energy packets of the size E=h*c/λ, where h is Planck’s constant. If a light particle of a certain energy E strikes the metal surface, this energy can be absorbed and can release an electron from the structure of the cathode material. For this to happen, however, the photon must have at least as much energy as that binding the electron to the material. This is the above-mentioned minimum energy described by the work function WA. Light particles with less energy are not capable of releasing any electrons at all, no matter how many of them hit the surface per time unit (intensity). As c and h are physical constants, the photon energy depends only on the wavelength λ, being inversely proportional, in fact. Above a certain wavelength λmin the energy of the photons is E=c/λmin, i.e. smaller than the work function, and the measuring instrument does not indicate any current.
Photons with a shorter wavelength can release electrons and we find that their kinetic energy is linearly related to the wavelength: Ekin = h*c/λ – WA, but independent of the radiation intensity (photon density). All that initially happens at higher intensities is that more free electrons are generated.
This relationship is shown for zinc in Figure 2. As can be seen from the graph on the right, the light has to be at least ca. 280 nm "short" for a photoelectric effect to be detectable. Zinc cathodes are therefore unsuitable for visible light. The work function of the material used must be as low as possible here. As can be seen from the periodic system, alkali metals are particularly suitable, as their outer electron is only very weakly bound to the atomic core. Therefore, the effective components of photocathodes are normally alkali metals or their mixtures (e.g. Cs, Rb, K, Na). In order to get good results for visible light too, semiconductor crystals are now also often used in the photocathode material (e.g. GaAsP). Many details can be found in the Hamamatsu Photomultiplier Manual [7]. This also applies to all the following sections, particularly for the properties of photomultipliers.
A key parameter for the choice of sensor is the quantum efficiency of the photocathode, i.e. the relationship between arriving photons and generated photoelectrons. Alkali photocathodes perform well between 300 nm and 600 nm, achieving efficiencies of almost 30 % in the blue range of the spectrum. Semiconductor variants achieve up to 50 % and can be used between 400 nm and 700 nm (GaAsP) or 900 nm (GaAs). Semiconductor photocathodes are therefore being increasingly used for life science applications requiring longer wavelengths, as optical scattering is a major problem with thick specimens that decreases with the fourth power of the wavelength.
For the huge diversity of applications there is therefore a great number of varieties differing in their spectral sensitivity, their quantum efficiency and their temporal resolution.
Multiplication (dynodes)
In the photocathode, an electron is released by every arriving and effective photon. Of course, this photoelectron is just as difficult to measure as a single photon. Unlike photons, however, electrons are extremely easy to manipulate: the energy of an electron can be increased by a DC voltage. If the free electron passes through a voltage U before being discharged, it absorbs the energy e*U that is added to the electron as kinetic energy in a vacuum tube. For a potential difference of 1000 volts, for instance, the electron receives 1000 eV (electron volts) of kinetic energy. A photon of 620 nm has about 2 eV. As can be seen, by accelerating the photoelectron through high voltage it is possible to assign far higher energy to the "one photon" signal than the photon itself contributes: this is a signal gain.
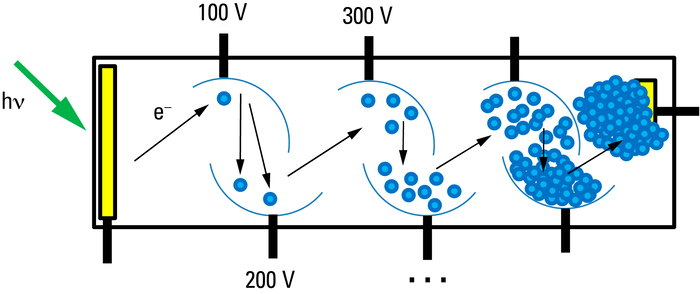
In a classic PMT, this gain is distributed among several stages. Behind the photocathode there is an electrode carrying a positive voltage of typically between 50 and 100 volts. The released photoelectron is attracted by this positive potential and accelerates in this direction until it finally hits the electrode. The kinetic energy is here converted into the release of several more electrons ("secondary electrons") – very similar to the process at the photocathode after absorption of a photon. Typical values lie between 2–4 secondary electrons.
To create a measurable charge, this process is now repeated several times in a cascade, so that for 3 secondary electrons per electrode (called dynode here), for example, a total of 3k electrons are released, where k represents the number of dynodes. Typically, PMTs have about 10 dynodes, which amounts to 310 = 60,000 electrons – a measurable charge of 10 fC.
The overall gain of the photomultiplier tube can be controlled via the total high voltage, which is normally distributed equally among the dynodes by a voltage divider. The higher the voltage, the greater the gain. The number of released electrons at each dynode is a mean value that can be continuously set through the voltage. This is why rather strange values such as "2.7 released electrons" are encountered here.
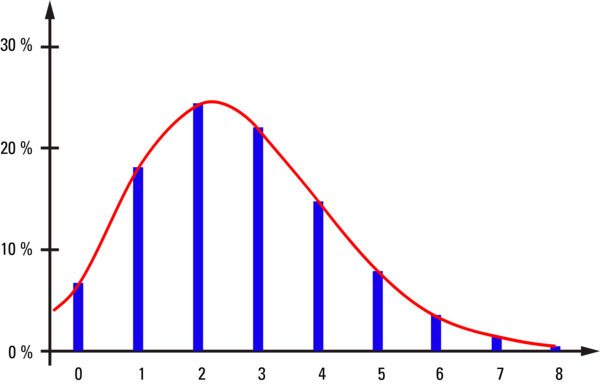
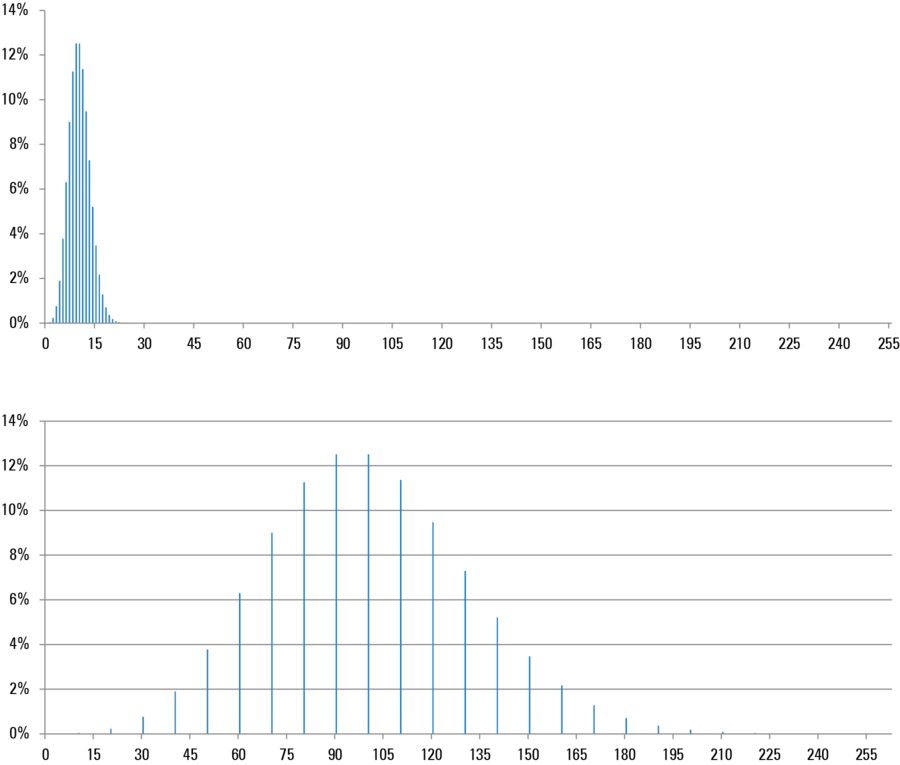
Figure 4 represents the frequency distribution for the example of 2.7 electrons, describing the number of electrons that are actually released by an electron arriving at a dynode. Most events yield one, two, three or four electrons, and occasionally even more. At the "late" dynodes, these events are averaged every time an electron shower from the preceding dynode arrives, and a gain of approx. 2.7x is obtained for every pulse. However, an average value cannot be taken at the first dynode, as only one single electron arrives there. The distribution in Figure 4 is therefore an approximation of the distribution of the pulse heights at the end of the PMT, showing that this value fluctuates by a factor of 4 to 5. Thus the amount of gain varies greatly from photon to photon. This is a significant contribution to noise in integrative measurement methods (see below). These different pulse heights also lead to discrimination problems when counting photons.
It is also quite possible that electrons do not hit the target (the next electrode). Depending on the stage at which this happens, the total charge becomes more inaccurate and the efficiency is diminished. Instead of the photocathode’s "quantum efficiency", the term "detection efficiency" is therefore often used, which considers losses along the whole chain.
The signal (anode)
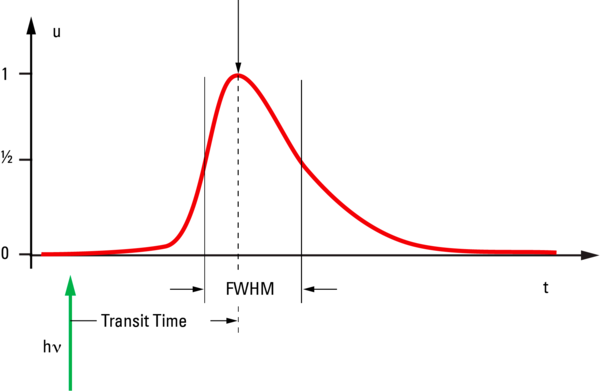
After being amplified by the high voltage stages, the electrons finally reach the anode, where the charge can be measured. Because of the different paths the electrons can take in the tube, they do not all arrive at the same time. Here too, the events are distributed, and the temporal distribution is reflected in the width of the ideal electric pulse. In fact, the pulse shape is greatly influenced by the measuring setup and the measured pulse width is a convolution of the distribution of the arriving charges with the attenuation properties of the downstream electronics.
To characterize the pulse shape, the full width half maximum (FWHM) is applied. For PMTs, this is roughly between 5 and 25 ns. Of course, the pulse is effective at the anode for longer than the full width half maximum, and for the time between 10 % rise and 90 % decay we can assume roughly twice the FWHM. However, the shape is not symmetrical; the rise time is two to three times faster than the decay time. To put it colloquially, this can be compared with the drops of water a dog shakes off its coat after having a bathe: first the number of drops increases quickly, and then it gradually decreases – because there are fewer and fewer left.
The time between the arrival of the photon at the cathode and the peak value of the output pulse is the transit time (TT), which is between about 15 and 70 ns, depending on the tube design. It is the time the signal is traveling in the tube. This time is randomly distributed around a mean value, too, and the transit time spread (TTS) is 1–10 ns. This is an important parameter for fluorescence lifetime applications, as it limits measurement accuracy.
Even if no photons hit the cathode at all, events will still be measured at the anode at a certain frequency. Most of them are triggered by thermal electrons emitted by the cathode. Thermal electrons from the dynodes can lead to minor events as well. These events are classed as "dark noise" and diminish contrast, which is a particular problem for weak signals as they can no longer be differentiated from the background. In a PMT of course, the noise of the photocathode and the early dynodes is amplified by the following stages. This is not the case in single-stage systems. A two-stage hybrid detector (see Chapter "The hybrid detector") therefore generates much less multiplicative noise.
Measurement methods and histograms
The charge cloud arriving at the anode produces a voltage pulse. More precisely, the applied positive potential of the high voltage is slightly attenuated in pulse form by the arriving negative charge. The charge is now measurable, but still very small. Careful design is therefore necessary to ensure that a significant measurement result is obtained. Basically, there are three different measurement concepts, which are outlined below. They are valid for all sensors, including the avalanche photodiodes and hybrid detectors described in Chapters "The avalanche photodiode" and "The hybrid detector". However, the methods are not equally well suited to all sensors.
We would also like to touch upon the subject of evaluation here, as users are not so much interested in how the sensor works as in the significance of these signals for their measurements and research.
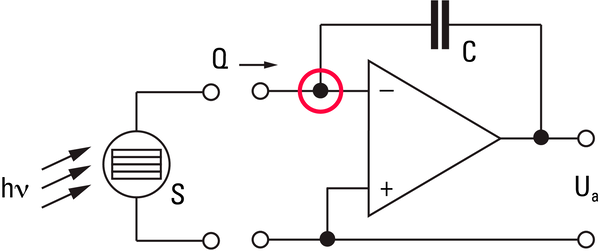
The charge amplifier
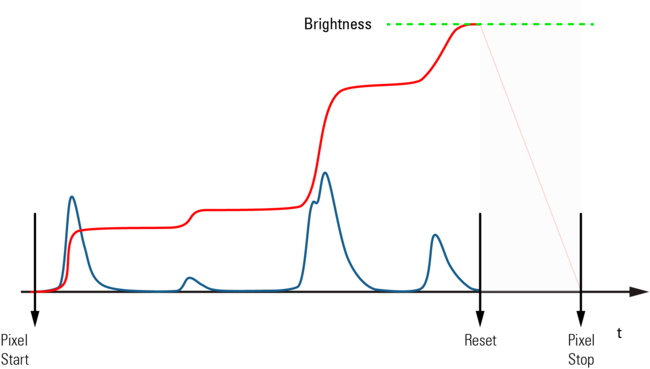
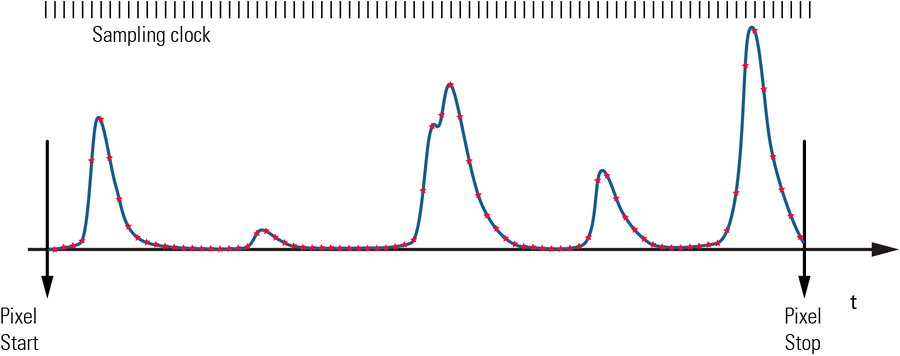
The conventional technique for measuring the PMT signal uses a so-called charge amplifier. In a scanning microscope, the illumination beam is constantly moved over the sample and every line has to be divided into the desired number of pixels. A typical recording for classic structural images takes about a second for 1000 lines per image and 1000 pixels per line. The recording time for one pixel thus takes roughly 1 microsecond. In this microsecond, all charges coming from the PMT are summed up in a capacitor as the graph in Figure 7 shows. A fraction of the total time is lost for resetting the charge amplifier, which has to start at zero again for the next pixel. The result is a voltage that is proportional to the total charge received from the PMT. This voltage is then converted into "gray values" by an analog-digital converter (ADC). Normally, 8-bit resolution is used, i.e. the gray values are integers between 0 and 255. By adjusting the high voltage at the PMT, it is possible to make sure the measured signal "fits" into these 8 bits, i.e. the entire dynamic range is exploited without the signal being cut off due to overload.
Obviously, these gray values do not indicate absolute brightness values, but just enable comparison of relative brightnesses in different image areas – or of the brightness of images taken at identical settings of the measurement technique. As described above, the signal height for each arriving photon varies considerably. During the time taken to measure the brightness in one image element, several and sometimes many photons arrive during the measuring time. The possible values are all the combinations of the charges for a single photon, which are quasi-continuously different, anyway. Therefore, the photon events for a cumulative measurement are completely blurred and there is a continuum of signal heights. The digitization process then turns this into 256 separate brightnesses, the gray values.
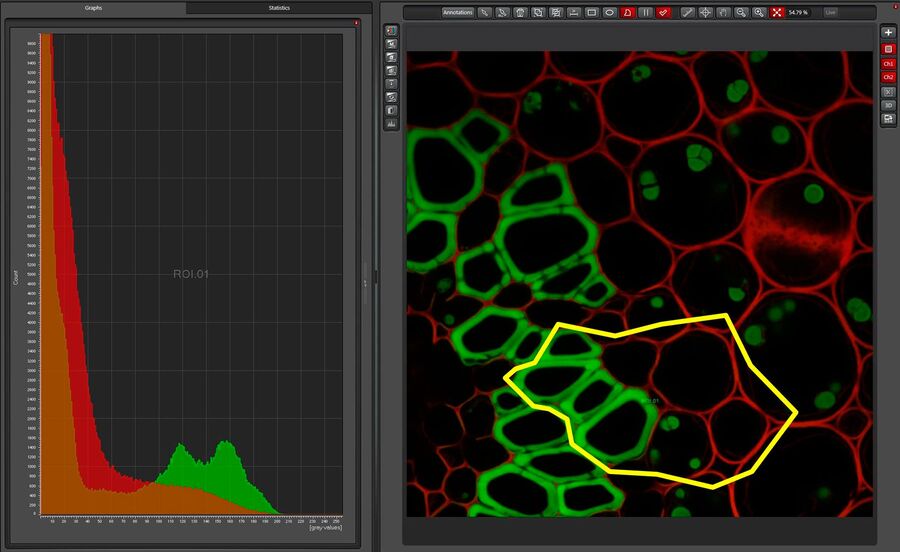
Of course, the experimenter is not usually interested in the brightness of discrete image elements, but in the intensity of a structure, such as a whole cell or tissue component. He or she therefore selects a region of interest (ROI) and calls up its brightness. Depending on the image resolution, which is mostly around 1000 x 1000 pixels, i.e. 1 megapixel, many hundreds or even thousands of image elements are combined in a single number. This mean value can then be compared with values from other structures, or be plotted as a temporal change in an experiment with living material, etc. It is also possible, for example, to analyze the brightness distribution in this area more precisely. To do this, a histogram is generated, counting the number of image elements that have a certain brightness. As there are 256 different brightnesses, the numbers from 0 to 255 are to be found on the x axis of an 8-bit histogram. Because of the digitization there are no intermediate values here. So strictly speaking there should not be a continuous line in a histogram. Also, the frequencies plotted on the y axis are only integers, which is logical as they represent the numbers of the image elements. A histogram of this type is shown in Figure 8. All sorts of details can be gleaned from this histogram; we are interested in three properties here.
If the brightness distribution is such that the curve is symmetrical, the mean brightness value is to be found at the histogram maximum. However, we frequently find a certain lopsidedness, indicating that the mean value is slightly to the left or right of the maximum.
For extreme brightness fluctuations, the curve becomes very "wide". If there was no variance at all, there would only be one gray value, and the "curve" would then be infinitely narrow. The width is therefore an indication of the variance. But it is not only the distribution of the number of photons arriving in an image element for each measurement time that influences this variance, but also the noise properties of the measuring system, here in particular the PMT, and also the electronics. Only when these noise portions are small enough is it possible to estimate the number of contributing photons derived from the ratio of the mean value to the width.
As the zero point is fixed by the setting of the electronics, it is not possible to deduce from a gray value histogram the proportion of PMT dark current in the background brightness.
For a usable image, a signal-to-noise ratio (SNR) of about 3 is needed. This is the case when 10 photons are registered in an image element. For a 1 megapixel image with a line frequency of 1 kHz, this is 10 million photons per second. As a rule, however, we try to manage with less light, as high illumination intensities destroy the fluorochromes, and the resulting fractions are often toxic chemicals for the living material. Therefore, the illumination is reduced until a good compromise is reached between image quality and sample stability. So frequently only an average of 1 … 3 photons and less is registered per pixel. Signals that are extremely weak but can still be evaluated have a mean value of significantly less than one photon per pixel.
Why do we get far more than 200 different gray values if we only have 10 photons? Wouldn’t 15 different brightness levels be enough? This would indeed be the case if each photon generated the same signal in the image. But, as we established above, the pulse heights vary tremendously (the intensity is noisy). If in a pixel the pulses from several photons are summed up, the possible number of brightness values is again multiplied. This is the reason for the large number of brightness levels. And the more levels we use (lower gray resolution with about 12 or 16 bits) the higher we rate the noise generated by the pulse variation. However, the result does not yield better information.
The histograms also supply further useful information. If, instead of exploiting the entire dynamic range of 0 to 255 during the recording, only the bottom tenth from 0 to 25 is used, the monitor image is extremely dark, as the monitor is only using the gray values from 0 to 25. We can only make the image brighter by "widening" the histogram, a common technique automatically offered by all digital cameras today. This is done by multiplying the brightness in each pixel by the same number Z for all pixels. In the case above, we would multiply all values by 10 to cover the range from 0 to 255. However, as there were originally only 25 x values, there are only 25 x values in the image result. So the histogram has gaps; in our example 9 values are missing between all the plotted gray values. The graphs therefore look rather "untidy", but are quite correct.
Although the charge amplifier was used for many years as a device for measuring PMT signals on confocal microscopes, it has now been mostly replaced by other techniques (see below). The charge amplifier delivers signals that are summed up over a whole pixel, so the result depends on the length of the pixel time. However, this pixel time changes if, for example, the scan format is changed, i.e. if only 100 instead of 1000 pixels per line are registered at the same scanning speed. The signal is then 10 times greater and necessitates adjustment of the high voltage on the PMT. Changing the scanning speed has the same effect. In addition, a small part of the measuring time is lost in each pixel because the resetting of the charge amplifier takes a certain amount of time. At high scanning speeds and high resolution the pixels are extremely short, and the reset loss becomes noticeable. This can be remedied by direct digitization.
Direct digitization
Modern digitization circuits are fast enough to convert the PMT signal directly into digital units. This is done by discharging the PMT charge via a suitably dimensioned resistor and converting the resulting voltage into gray values at a high clock rate. The data of a single image element is immediately averaged while it is being recorded, and the image is consequently given gray values that genuinely represent the intensity of the sample, however long it takes to record an image element. The high voltage at the PMT does not need readjusting and the brightnesses in particular can be compared directly. There is no time lost for resetting, either.
The histograms look exactly the same for direct digitization as when a charge amplifier is used and basically contain the same information. After all, the averaging method basically adds up the measurement data as well, but scales them immediately on the correct time axis. The scan zoom does not change the image brightness here either, except for the real changes in brightness caused, for example, by different degrees of fluorochrome bleaching – but that is valuable information, not a measuring artifact. Bleaching can be immediately quantified here, too.
A further advantage of this technique is that there is no dead time spent emptying a memory. This results in a better signal-to-noise ratio for extremely short pixel times.
Photon counting
We now have splendid clear and simple histograms to describe intensities. Interestingly, however, the world is far from being so smooth and continuous. As Max Planck [7] involuntarily discovered, light does not exist in a continuously intense form. This is why with our detectors we measure single events, the arrival of photons, rather than continuous intensities. The apparent continuum is the result of metrological vagueness: the histograms of analog measurements with a PMT show the merging of blurred measurements. As we already mentioned, a photon at the PMT generates a pulse of varying width that first rises in intensity and then falls. By integrating or averaging a large number of pulses of different widths and heights, an apparently continuous brightness histogram is obtained in which any intensity values can occur. What’s more, the number of these intensity values depends on the arbitrary "gray depth" setting for data recording. In reality, however, this is by no means the case. On closer consideration, the brightness in a pixel cannot be represented by a rational number. It can only be an integer, in fact it can only be the exact number of photons that arrived at the detector during the measuring time in this pixel*. So rather than integrating or averaging the charge (i.e. the area under the pulse curve) of each pulse, it would be desirable to count the charge pulses arriving at the anode without evaluating the pulse size. This would solve a major part of the noise problem.
* In fact, the light intensity also depends on the color of the photons, and this will also slightly influence the pulse heights. However, this energy difference accounts for only about 2 eV for the entire range. Compared with about 80V at the first dynode, this is negligible. For the hybrid detectors (HyD) discussed below, this variation is even about a hundred times less significant.
The same applies for the initial velocity of the photoelectrons, which, as we mentioned, can leave the cathode in any direction. Some of them fly in the desired direction, but others have to be accelerated by a change of direction that reduces the kinetic energy when they hit the dynode. Here too, the variations are only in the range of ± 2 eV.
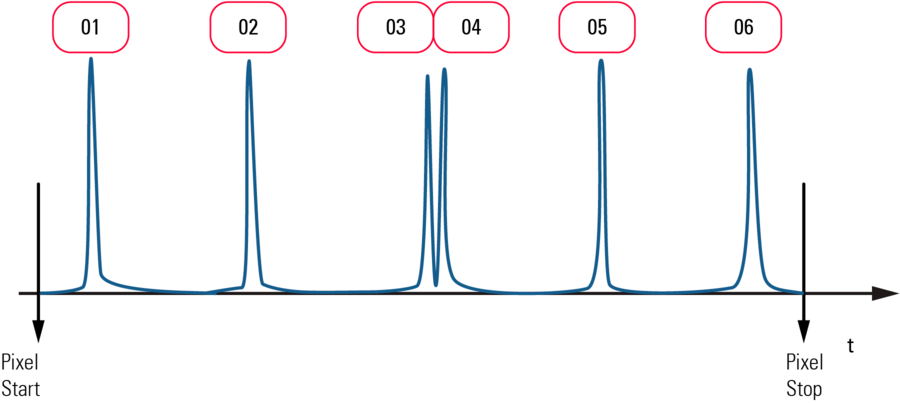
Such counters are a standard in electronics nowadays. The height or a slope of the pulse is used to activate a trigger that increments the counter by 1 each time. At the end of the pixel, the counter is reset to 0 (this takes next to no time) and the counter begins again. However, the limitations of this method are instantly apparent in Figure 11: the pulses naturally have to be separately discernible. If a second pulse occurs during the first one, only one pulse is detected and the subsequently measured brightness is too low. Whether the pulses are separated or not depends on the interval between the pulses and on the pulse width. Wide pulses allow only dim brightnesses for the photon counting method, as otherwise the pulses follow each other too quickly with the risk of overlay. Narrow pulses can yield good counting results even at higher intensities, i.e. at shorter pulse intervals.
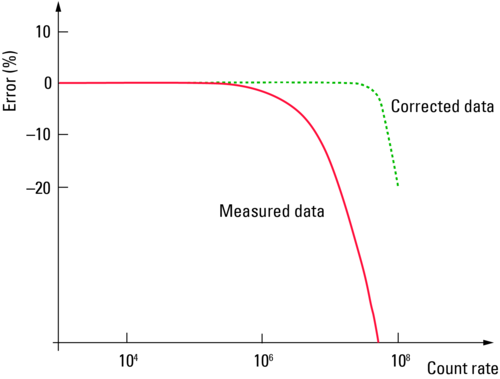
A typical PMT delivers pulses of a separable width of about 20 ns. If photons always occurred at the same time intervals, counting rates of up to 50 million per second (50 Mcps) could be realized. As they arrive stochastically, however, overlapping is much more probable, and the highest counting rate is reduced. By the highest counting rate, we mean that the relationship between the number of actually triggered photo electrons and the measured number of pulses is no longer linear above this counting rate. Admittedly, this is an arbitrary definition depending on the error tolerance. If a deviation of only 1 % is allowed, the linearity ends at 0.5 Mcps, for 10 % at 5 Mpcs. An accuracy of one per cent is unattainable in everyday practice anyway, whereas 10 per cent is above the tolerance threshold. The threshold can be set at 6 %, for example, to obtain a useful measurement up to counting rates of just over 10 Mcps.
If we assume for a moment that there are no brightness fluctuations (e.g. by illuminating a fixed point, without scanning movement) the photons arrive at the detector on average uniformly, but stochastically. In such a Poisson process, the time intervals between photons can be described by an exponential distribution. We need not go into detail here, suffice it to say that such a process can be described in exact mathematical terms. To a certain extent we can use it to compute the error resulting from pulse overlay that causes the deviation from linearity. If the error is known, however, we can use the measured number of pulses to count back to the actual number of arriving pulses. This works up to about five times the pulse rate at which the error became significant without correction. Therefore, this correction is called linearization. It is a well-known and well described method for extending the measurement range [7].
Fig. 12: Linearization of the counting rates by correcting the statistic probabilities. Note the logarithmic x axis [6].
Instead of the originally counted pulses (corresponding to the photons), this linearization, just like widening, yields fractions as well as integers in the computation. This in turn impacts the histogram, which naturally plots only integers such as gray values. In any case, the widths of these energy channels are normally always constant, and it is always possible to convert any fractions into integers, e.g. by beginning at 0 and then simply continuing to count. Linearization therefore leads to the occurrence of beat effects in the histograms, so that individual energy values protrude far beyond the envelope of the histogram. Although irritating at first, it is an exact representation of the statistically corrected photon numbers.
The avalanche photodiode
Of course, light-sensitive components that can be used to measure intensities have meanwhile been produced in semiconductor technology, too. The instrument that can be most easily compared to a photomultiplier is the avalanche photodiode (APD).
Turning photons into charge pairs
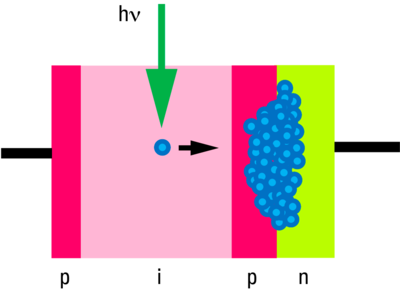
To measure light with semiconductors, the inner photoelectric effect is used. This entails generating a charge pair (free electron and diffusible "hole") in a very weakly doped semiconductor material after the absorption of a photon. The absorbing layer is embedded between a p- and an n-doped layer, thereby having an effect like the enlargement of the depletion region that would form at a direct pn junction. The layer is called "i" layer because it only demonstrates intrinsic conductivity. These semiconductor systems are called pin diodes due to the order in which the layers are arranged. If a reverse-biased voltage is applied to the electrodes of such a photodiode, a current will flow that over a wide range is proportional to the intensity of the incident light. However, such a diode is not sensitive enough for weak signals and has too much noise.
The avalanche effect
To be able to measure even weak signals, an extra layer is added to the pin arrangement: another highly doped p layer is inserted between the i and the n layer. The extremely high field strengths formed here cause the charges to accelerate rapidly and emit their energy as they knock against the grid elements, generating further charges (the reason for the comparison with the PMT). These charges are accelerated, too, causing the process to swell like an avalanche and lead to a pulse in the measurement circuit. If the charges are moderate, the avalanche stops by itself, and a gain of up to 102 can be attained. At extremely high reverse voltages, massive gain is achieved (up to 108), but the current has to be actively interrupted to avoid destroying the component. This latter case is called "Geiger mode", as it is suitable for detecting single photons without additional amplification. The disadvantage of the Geiger mode is the long deadtime period after a measured event. Generally, therefore, this mode is not suitable for image recording.
How it differs from the PMT
Unlike photomultiplier tubes, avalanche photodiodes only have a small dynamic range, so one always has to make sure that the intensity of the light being measured is not too high. The gain in non-Geiger mode is between 100x and 1000x, depending on the voltage applied. On the other hand, this type of sensor has extremely slight dark current, making it suitable for weak signals that would be lost in background noise if the dark current was too high. The spectral sensitivity covers a wide range of 300 nm to over 1000 nm, which explains why, for red fluorescence emissions in particular, APDs are used for image recording, too. In spite of the extremely high sensitivity in the red range, the thermal noise is still relatively small. This noise depends on the surface area of the sensor, which is 0.1 mm2 at most for an APD, whereas the surface area of PMT sensors can be up to 10 mm2.
APDs generate very narrow pulses, an important property for photon counting. This can only be utilized in non-Geiger mode, though, as otherwise the advantage is lost due to the very long deadtime periods (several 10s of ns).
The hybrid detector
It would be good to be able to unite the high dynamics of a PMT with the speed and low noise of an APD. This is exactly what has been achieved with a chimera technology consisting of a vacuum tube and a semiconductor component. The result is a hybrid detector (HyD; also HPD: Hybrid Photo Detector or HPMT: Hybrid Photo Multiplier Tube).
The combination of the two technologies in this component really has resulted in a sensor that combines the best characteristics of a PMT and an APD.
Design
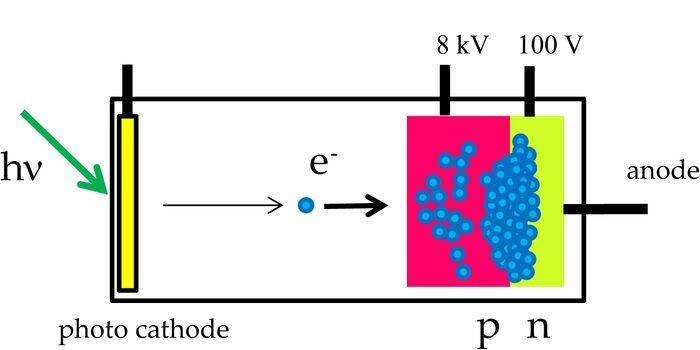
The "input" of an HyD is identical to that of a PMT: a photocathode in an evacuated tube can release a photoelectron by absorption of a photon. As a rule, GaAsP cathodes are used – these are also the most suitable cathodes for PMTs used in biomedical fluorescence applications. Unlike the PMT, however, this photoelectron is massively accelerated in one single step rather than in stages, passing through a potential difference of over 8000 volts.
Here already, we can see that the differences in the relative pulse height are much less than for a PMT, for which the acceleration voltage as far as the first dynode is about 100 volts. As described in Chapter "The photomultiplier tube", the number of electrons released at the first dynode is between 2 and 4, with an expected variance of 1 to 2 electrons. This is why the pulse heights there usually vary by a factor of 3–5. By contrast, the photoelectrons in a hybrid detector are accelerated by 8 kV. From the kinetic energy, approx. 1500 secondary electrons are obtained. There are therefore variations of 40 electrons (√1500). Although this is, of course, more than 2–4 electrons, it is only 3 % of 1500. The output pulses are therefore extremely homogeneous and a much more accurate representation of the illumination energy.
Now, the highly accelerated photoelectron does not hit a dynode (which could not cope with such high energies), but a semiconductor. Here the energy is converted into a great number of charge pairs (approx. 1500, as mentioned above). An applied voltage makes this charge move in the direction of a multiplication layer as described for the APD (avalanche effect). Here, the signal is amplified again by about 100x and thus becomes a measurable pulse.
Data recording with a HyD
Due to the single-step acceleration and the subsequent direct amplification, there is much less variance at the trajectories of the charges, which means that the pulses are much sharper than with a PMT: the pulse width is reduced by about 20x and is about 1 ns (currently close to ½ ns).
Furthermore, due to the absence of dynodes and the much smaller size of the photocathode, there are far fewer dark events. Compared to a photomultiplier tube, background noise is also greatly reduced. Besides improving the contrast of the recorded images, this also allows a greater number of images to be averaged or accumulated. As the background is almost totally black, it still remains black when a large number of images are combined into one, which makes it possible to significantly reduce signal noise at high contrast.
The hybrid detector therefore offers myriad advantages. Its homogeneous and narrow pulses allow photon counting with light currents that would soon oversaturate a PMT. It therefore makes sense to use hybrid detectors in photon counting mode for "ordinary" image recording, too. After all, as described in Chapter "Photon counting", photon counting has a lot of advantages compared to analog detection techniques.
Consequently, the evaluation does not yield histograms "smudged" with noise and quasi-continuous histograms, but, as is to be expected, well defined frequencies of only a few photons. Figure 9 actually shows a histogram of this type. At the top you see the Poisson distribution for a mean value of 10 photons per pixel.
Utilizing hybrid detectors, the Leica TCS SP8 system offers a free choice of three different data recording techniques. First, the raw data of the photon counting can be used as image information ("Photon Counting" mode). As linearization methods are not used here, the maximum counting rate is lower than for linearized data, but still significantly higher than for conventional photomultipliers. A rate of around 60 Mcps is obtained (cf. Chapter "Photon counting" for an explanation).
If the counted events are corrected by the mathematical linearization method described above, the maximum counting rate is improved by a factor of 5 and brightnesses of up to 300 Mcps can be recorded. Here, photons can be converted into values that may not necessarily be integers, so it is a good idea to carry out a scaling process right away to make the brightnesses comparable with conventional sensors and suitable for a balanced display on a monitor. This method is applied as standard. Note that the histograms may look "odd" due to widening and rounding effects. The data measured when evaluating image brightness are still correct, though.
For better perceptibility of the total dynamic range used, the values can also be changed to reduce the effect of bright pixels and increase the effect of dark pixels. This corresponds to the results of HDR rendering. Designated "Bright R", this mode is used to display images that exhibit great brightness differences so that there is no glare in bright image areas and dark areas remain visible. An example of this would be neurons with a great amount of dye in the cell soma and extremely thin dendrites.
| Mode | Scaling | Linearization | Augmented dynamics |
|---|---|---|---|
| Photon counting | no | no | no |
| Standard | yes | yes | no |
| Bright R | yes | no | yes |
References
- Becquerel AE: Mémoire sur les effets électriques produits sous l’influence des rayons solaires. Comptes Rendus 9: 561–67 (1839).
- Hertz HR: Ueber den Einfluss des ultravioletten Lichtes auf die electrische Entladung. Annalen der Physik 267 (8): 983–1000 (1887).
- Hallwachs WLF: Ueber die Electrisierung von Metallplatten durch Bestrahlung mit electrischem Licht. Annalen der Physik 34: 731–34 (1888).
- Einstein A: Ueber einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. Annalen der Physik 322 (6): 132–48 (1905).
- Newton I: Opticks. Or, A Treatise of the Reflections, Refractions, Inflections and Colours of Light (1704).
- Planck M: Ueber irreversible Strahlungsvorgänge. Ann. Phys, 1: 69–122 (1900).
- Hamamatsu Photonics KK: Photomultiplier Tubes – Basics and Applications. Ed. 3a: 310 (2007).