3D point spread function (PSF) and Full Width Half Maximum (FWHM)
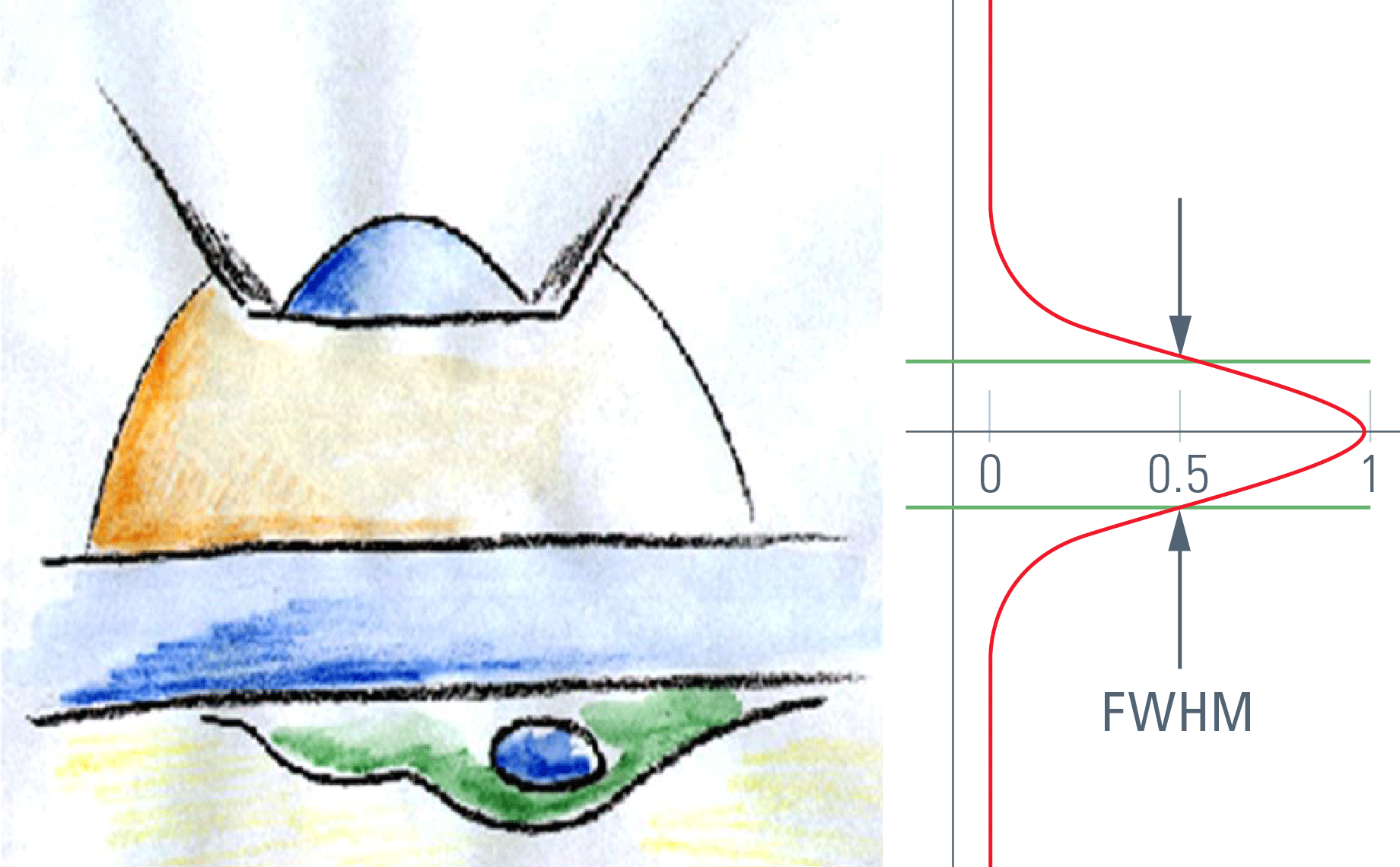
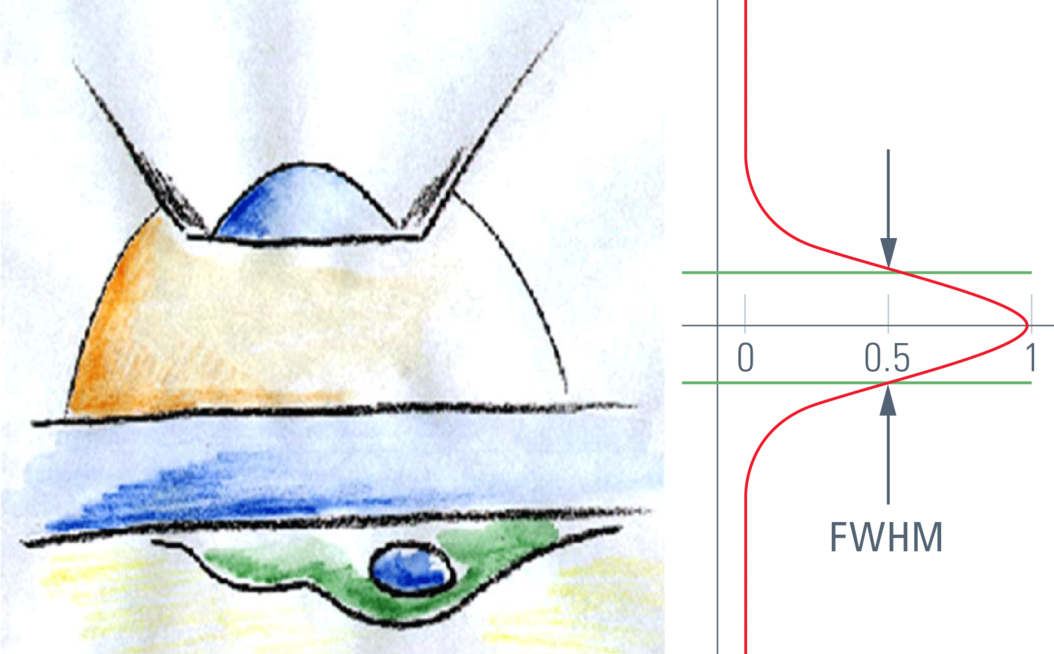
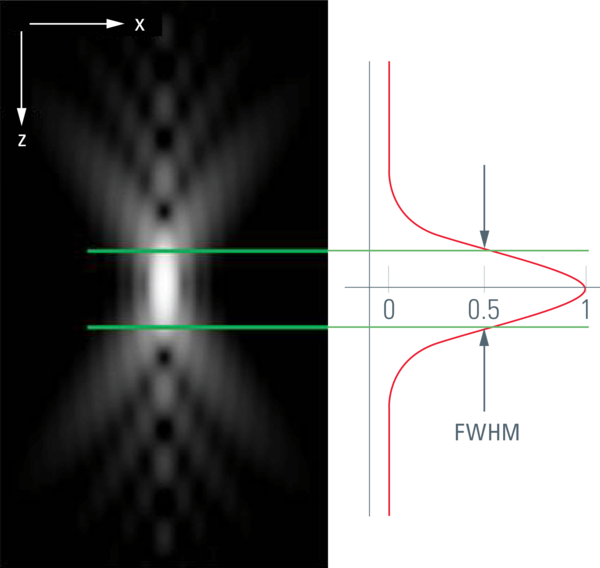
The image of a point (spot) that is created by an optical system is called the "point spread function" (PSF). The point spread function describes the distribution in three dimensions of light originating from a dimension-less spot. The core of this diffraction pattern has an ellipsoid shape, and that controls the optical resolution. The radial dimension rules the lateral resolution; the axial dimension rules the depth of focus and thus the slicing performance.
For confocal sectioning, the goal is to transmit only the inner core of the PSF, which defines the optical section. As a matter of fact, the pinhole diameter controls how much light from outside the core is transmitted. The optical section that is in the range of the size of the diffraction pattern is thus obviously not sharp-edged like a slice of bread, but is characterized by a comparably flattish slope. The distance in z that connects the 50 % intensities on both sides of an intensity profile is called the "full width half maximum" (FWHM), and by convention this is used as a measure of the thickness of optical sections. The optical sectioning performance is typically measured by focusing through a surface mirror that models an infinitely thin structure in z. This method is (comparably) easy and is used to examine the performance of confocal microscope systems. Alternatively, and more realistically, z sectioning performance is measured with fluorochromated latex beads (see Figure 1). The fluorescent beads allow the performance to be measured in non-coherent conditions, which is true for fluorescence imaging and thus fits the vast majority of confocal applications in biomedical sciences. The diffraction-limited optical sections in reflected light mode (mirror) are significantly thinner as compared to sections in fluorescence mode. This is important to keep in mind if comparing figures from literature.
Parameters controlling the thickness of optical sections
Under ideal conditions, the thinnest section achievable would only depend on limitations by optical diffraction. The most obvious is the wavelength, which controls the size of the PSF proportionally: the shorter the wavelength, the thinner the slice. We can assume the wavelength of the excitation light to be limiting (rather than that of the emission), as there will be no emission from outside the illuminated space. The second parameter is the aperture of the objective lens (numerical aperture, NA): the higher the NA (wider angle for collection of information), the thinner the optical section. Also, the refractive index of the sample affects the axial resolution and consequently the sectioning performance. The dependence of the slice’s size dz on these parameters is given by the formula Figure 2.
The third parameter is the pinhole diameter in the detection path, which is assumed to be zero for the formula given above. Therefore, this formula gives the best value one can expect for fluorescence imaging – and is of course only of theoretical interest: a pinhole with zero diameter would not generate bright images!
Critical comments on optical section thickness
The numerical aperture NA has a significant (1/square) impact on the slice thickness. The radial extension of the psf depends linearly on the NA. Consequently, for low-NA lenses, the PSF core becomes very elongated and the slices very thick. Most applications therefore use immersion lenses with NA > 1, where the ratio of xy and z dimensions approach roughly a factor of 2. As a rule of thumb, the z section with high-NA lenses is roughly double the xy resolution.
Theoretical considerations help to estimate the performance of optical systems. In reality, both the instrument and the sample introduce deviations from the calculated figures. The instrument must be adjusted and operated carefully for optimal performance. And the sample itself is the enemy of resolution, especially if it comes to deeper imaging. Extreme care therefore has to be taken for refractive index matching, correct and constant temperature and proper coverslip selection. The theory will give a rule of thumb, but sample and setting may introduce significant deviations – often inescapable, as biological samples are more complex than crystals (– or the vacuum).
References
- Sheppard CJR: Scanning optical microscopy. In: Barer R and Cosslett VE (eds), Advances in Optical and Electron Microscopy 10 (1987). Academic Press, London UK.
- Wilson T: Confocal Microscopy. Academic Press, London UK (1990).
- Corle TR and Kino GS: Confocal Scanning Optical Microscopy and Related Imaging Systems. Academic Press, San Diego USA (1996).
- Borlinghaus RT and Gröbler B.: Basic Principles and Applications of Confocal Laser Scanning Microscopy. In Isenberg G (ed): Modern Optics, Electronics, and High Precision Techniques in Cell Biology, 35–53 (1997). Springer Heidelberg.
- Cox G: Optical Imaging Techniques in Cell Biology. Taylor & Francis, Boca Raton USA (2007).