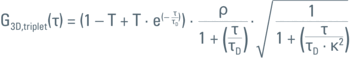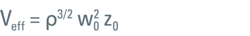FCS – the methodology
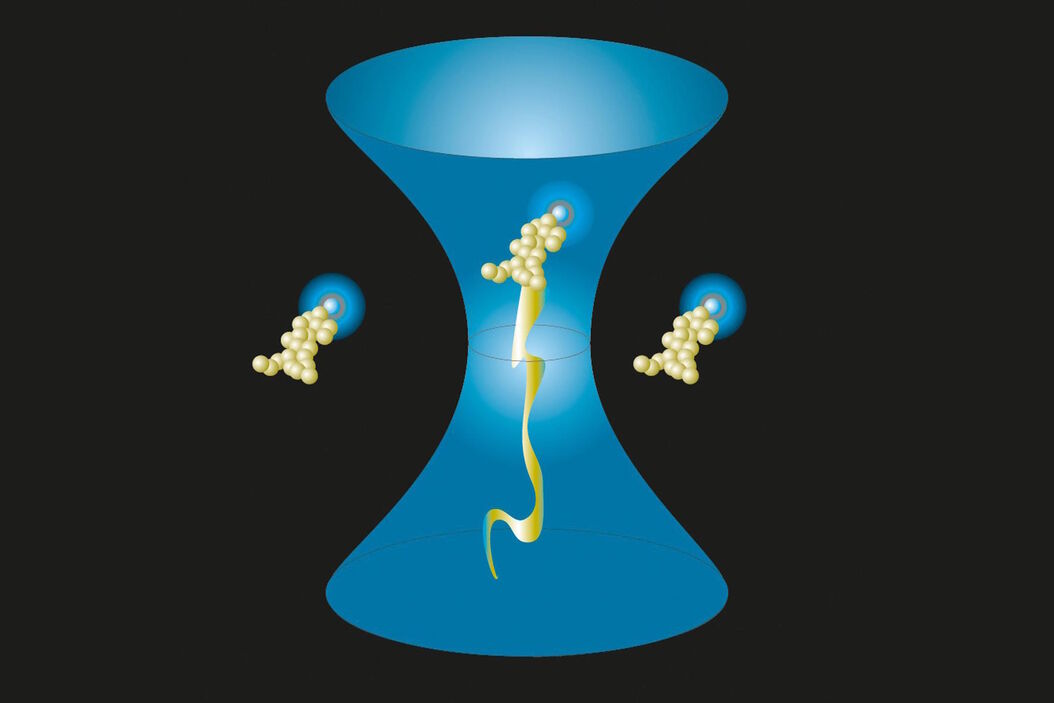
FCS is a spectroscopic method. The "cuvette" in this case is a diffraction limited spot (Figure 1). Thus, the reason one uses a microscope is to have a high numerical aperture lens which focuses the beam into a femtoliter sized spot. A welcome side-effect of having a microscope is being able to take an image of the sample for referencing and positioning of the measurement spot (ROI). In FCS the primary read-out is fluorescence intensity over time (fluorescence trace or intensity trace). The fluorescence fluctuations implicitly encode particle numbers (i.e. amplitude of fluctuations) and particle dwell times (i.e frequency of fluctuations), see Figure 2. One performs an autocorrelation analysis ("test for self-similarity") and curve fitting to obtain these parameters quantitatively (Figures 3 and 4). The geometry of excitation and detection light in the confocal spot roughly follows a three-dimensional normal distribution. By approximating it with a Gaussian function one can find an analytical model for the FCS autocorrelation function. Its parameters and their physical meaning are summarized in Table 1.
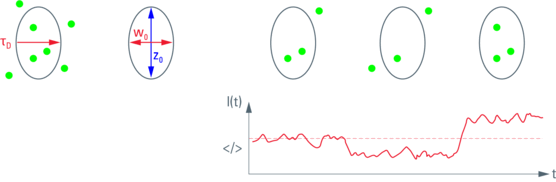
Fig. 1 (left): Observation volume and important parameters. The diffusion time τD indicates the time molecules spend within the observation volume, i.e. how long it takes to diffuse laterally. The lateral extension (beam waist), w0, and the axial extension, z0, of the observation volume are given (right hand side). Their ratio z0/w0 is the excentricity or structure parameter, κ.
Fig. 2 (right): Fluorescence intensity trace. Movement of molecules into and out of the observation volume (upper row) leads to random fluctuations of fluorescence intensity.
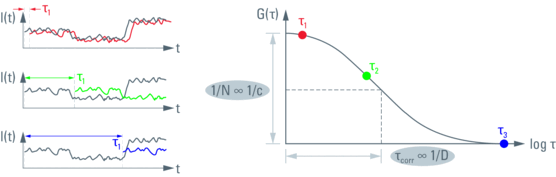
Fig. 3 (left): Principle of autocorrelation. The fluorescence trace gets copied, multiplied by itself and the results summed up. This is done for multiple times, each time shifting the second data set by an increment τi (lag time). After small lag times the data is still self similar, resulting in a larger sum (red). Longer shifts mean smaller numbers (green and blue). This technique analyzes the underlying information on the frequency of molecules diffusing through the observation volume.
Fig. 4 (right): Autocorrelation function G(τ) gets plotted over the lag time t. G(τi) representing different lag times is plotted qualitatively from Figure 3 (red, green and blue dots). The amplitude at G(0) encodes the inverse of the particle number N. The time at half-maximal amplitude (point of infl ection) yields the diffusion time τD, also referred to as correlation time. From these numbers one can obtain concentration c and diffusion coefficient D using proper calibration.
For details on the “anatomy” of an FCS curve, i.e which processes are observed at what time domain, as well as for a general introduction to the topic, please refer to an online article by Petra Schwille and Elke Haustein [3].
| Parameter | Name | Significance |
| ρ | Current amplitude | G(0) amplitude contributed by a molecular species |
| τD | Diffusion time | Time molecules spend inside Veff |
| τT | Triplet time | Time molecules spend in dark state |
| T | Triplet fraction | Fraction of molecules in dark state |
| κ | Structure parameter | Excentricity of Veff, κ = z0/w0 |
Table 1: Parameters of 3D Gaussian Triplet model for data fitting with one molecular species and normal diffusion in 3D.
Calibration – from relative to absolute numbers
The two main parameters of interest in FCS measurements are the diffusion coefficient, τD , and the number of molecules, N. They directly relate to the diffusion coefficient, D, and the concentration, c, respectively. However, both τD and N, are relative numbers influenced by each individual instrument and several experimental parameters. To obtain the absolute numbers D and c is the purpose of instrument calibration.
The effective volume
Both parameters, diffusion time and number of molecules, depend on the size of the observation volume. It shall be referred to here as the effective volume, Veff. Calibration is about determining the size of Veff.
Calibration strategies
Three approaches for determining Veff are described in the literature:
- Measurement of the confocal volume using fluorescent beads in 3D and fitting a 3D Gaussian function.
- Preparing a concentration series and plotting N as a function of c. The slope yields Veff.
- Measurement of known dye with known D. Curve fitting yields τD and κ, from which Veff can be calculated.
Each approach has its drawbacks and benefits. For example 1. gives an exact description of the confocal volume, providing details on how well the 3D Gaussian approximation holds. It is not measured in aqueous solution like the actual measurement. The second approach is modelfree, making no assumptions about the geometry of Veff or the diffusion model. It thus contains no information on its shape, it is laborious and may suffer from dark states if no curve fi tting is used to estimate N, but it works over a large range of concentrations. The last approach works under conditions very close to the actual FCS measurement, contains some information on the geometry of Veff and can be easily implemented. In the following we shall examine this strategy step by step. For a detailed comparison of all three approaches please refer to [1].
Effective volume obtained by curve fitting
Since this approach is based on curve fitting, the quality of the results depends very strongly on how well the model describes the reality. The strongest assumption made is that of a 3D Gaussian geometry of Veff, as is commonly done in FCS analysis. Misalignment of the system will therefore cause this assumption to be violated. Also, a good signal-to-noise ratio of the autocorrelation is required, because τD and κ are both determined from fitting the same data set. This is best fulfilled by bright, photostable dyes in water at a concentration range from 0.1 nM up to 10 nM [1]. The effective volume is then given as in Equation 1.
Equation 1: Effective volume. Size of observation volume relevant to FCS measurements with w0 as lateral and z0 as axial extension. Both parameters depend on τD and κ obtained by curve fitting of a calibration measurement. Please note that Veff is larger than the confocal volume typically referred to in the literature by a factor of 2^(3/2) ~ 2.8.
References
- Madge D, Elson E, Webb WW: Thermodynamic fluctuations in a reacting system – Measurement by fluorescence correlation spectroscopy. Phys. Rev. Lett. 29 (1972) 705–708
- Rigler R, Widengren J: Ultrasensitive detection of single molecules by fluorescence correlation spectroscopy. Bioscience 3 (1990) 180–183