Estimations of ion concentrations and pH or voltage changes by measuring fluorophore emission shifts
Research activities are increasingly focusing on the identification and the spatial and temporal distribution of e.g. local “hot spots” for dynamic changes in ion concentration, voltage or pH in a cell or a cellular network. Such “hot spots” are often localized in specialized parts of a cell or in certain cells in a cellular network. Additionally, these areas often have different properties compared to the rest of the specimen in terms of cell metabolism or structure. Conventional fluorophores used to investigate dynamic physiological states change their emission intensity upon ion binding, pH change or voltage change (e.g. fluo-4 has increased emission upon calcium binding). However, these markers do not take into account that differences in structure, diameter or marker uptake/expression can cause changes in the quantity of emitted light that are not in correlation with the actual ion concentration, voltage or pH. To quantitatively and comparably detect the changes in cellular structures or different cells, a method insensitive to structure diameter and fluorophore concentration is needed. In contrast to non-ratiometric imaging methods, ratiometric imaging offers the opportunity to reproducibly measure absolute intracellular ion, voltage and pH levels/changes with respect to cell diameter, fluorophore concentration and optical properties of the imaging setup. However, ratiometric imaging depends on a fast change of excitation wavelength or the detected wavelength, a strong light source, excellent transmission of optical components and fast signal detection. The recent development of ultrafast filter wheels, UV-light optimized objectives, highly sensitive fluorophores and new CCD cameras allows affordable quantitative high speed live cell imaging in high spatial resolution.
Dual wavelength excitation/detection is the key for measuring emission shifts of fluorophores
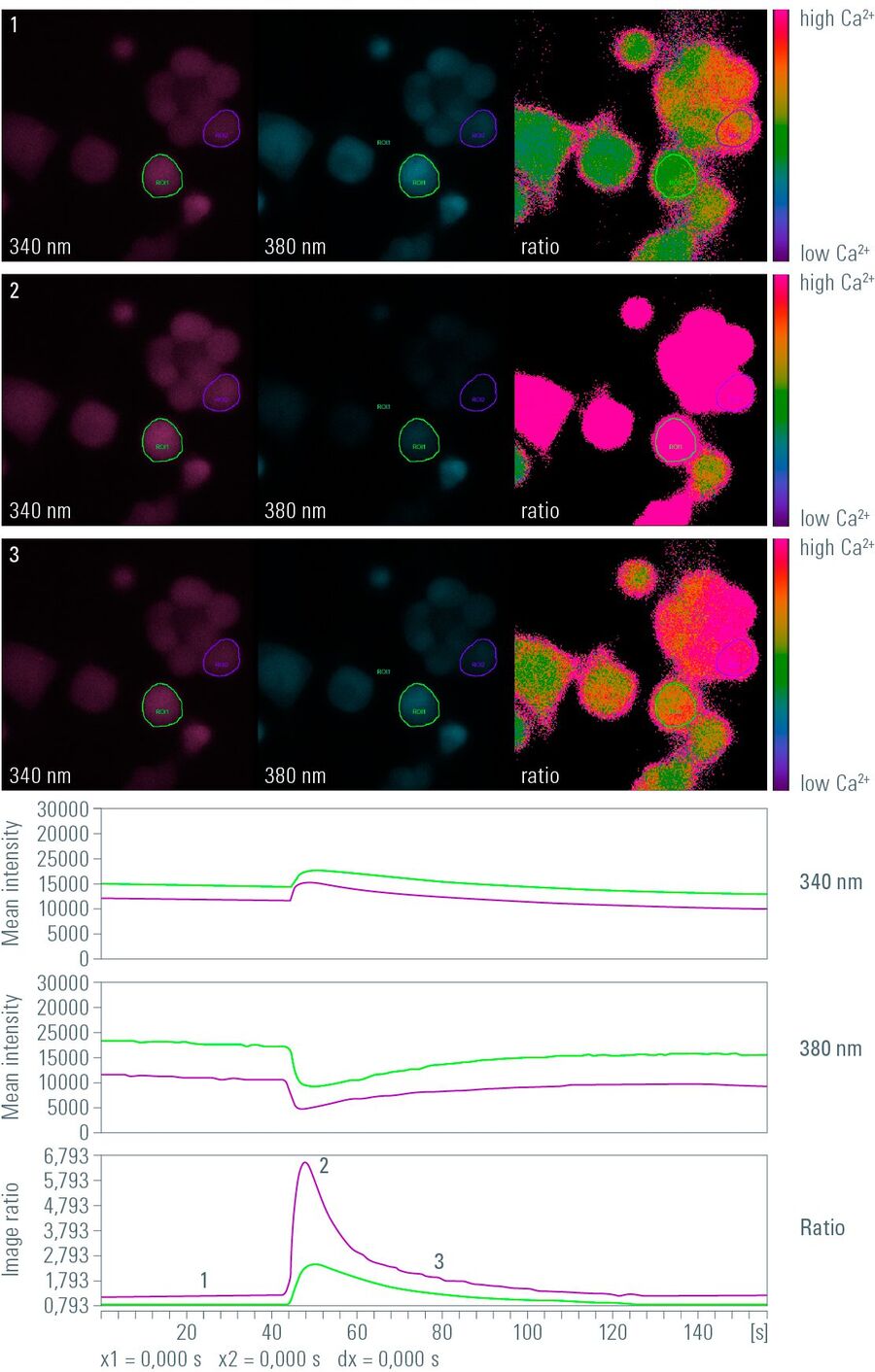
As mentioned above, in ratiometric imaging an emission shift instead of mere intensity change is imaged. To measure emission shifts, intensity changes of a fluorophore or fluorophore combination have to be measured either by using two different excitation wavelengths or by detecting at two different emission wavelengths. In the case of the commonly used calcium imaging dye fura-2, the dye has to be excited with light at wavelengths of 340 nm and 380 nm and the detection wavelength is 510 nm. In contrast to that, the calcium imaging dye indo-1 is usually excited with light at 350 nm wavelength and the detection wavelengths are 405 nm and 485 nm.
But why is dual excitation or emission detection necessary? Why not simply measure changes in fluorophore intensity?
Given an experiment where fluorophores are used to detect changes in ion levels, voltage or pH, the intensity of emitted fluorescence light depends on several properties. These are described in the equation below:
F = fluorescence intensity; c = fluorophore concentration; d = diameter of specimen (z-axis); K = optical constants of components in the light pathway (cell properties, objectives, filters etc.); f(x) describes the emission behavior of a given fluorophore if e.g. ions are bound or voltage/pH changes occur.
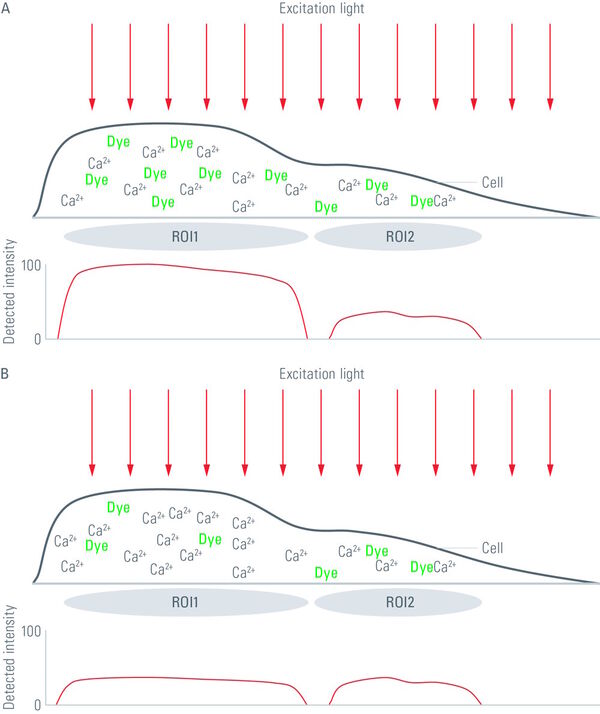
The equation shows that the light intensity very much depends on the amount of fluorophore in the optical path. The amount of fluorophore in the optical path depends on the actual concentration (c) of fluorophore(s) in the cell (determined by marker uptake or expression) and the diameter of the specimen (d) that is imaged. This makes it hard to directly estimate the concentration of an investigated ion, pH levels or voltage changes by simply observing the fluorescence intensity, e.g. one cannot state: “Intensity of 100 equals 100 nM of free calcium in a cell”. Specimen diameter (d), fluorophore concentration (c) and optical properties of the specimen and setup (K) are hardly measurable but substantially influence the overall intensity detected. Additionally, it has to be kept in mind that the formula shown above is true for any given point in the specimen. As the diameter (d) and the fluorophore concentration (c) are not homogeneous throughout one specimen or even within a single cell, the values for c and d might be different for every pixel in an acquired image of the specimen. If e.g. in point “A” in the specimen the diameter of the cell is rather high and free calcium rather low, light intensity might be the same as in a point “B”, where it is the opposite. The experimenter however, could wrongly conclude that the calcium concentration is similar in both places, as detected fluorescence light intensity is similar.
To overcome these issues and for precise measurements of absolute ion concentrations, pH levels or voltage, ratiometric imaging has been developed. All ratiometric methods have in common that the intensity of emitted light is measured twice and a ratio (R) of these intensities is calculated. Depending on the fluorophore or the fluorophore combination used, the fluorophores are either excited with light of two different wavelengths and the emission intensity is measured at one wavelength – or the fluorophore or fluorophore combination is excited with light of one wavelength and the emission is measured at two different wavelengths. This simply means that two gray value images are acquired and a ratio image is calculated from them. The two gray value images usually differ in their intensity, but the intensity of every single pixel in the image can be described by the formula shown below:
F = fluorescence intensity; c = fluorophore concentration; d = diameter of specimen (z-axis); K = optical constants of components in the light pathway (cell properties, objectives, filters etc.); f(x) describes the emission behavior of a given fluorophore if e.g. ions are bound or voltage/pH changes occur.
As the name ratio imaging implies, a ratio value for every pixel of the two simultaneously acquired images is calculated. For example, if the very commonly used calcium sensitive dye Fura-2 (excitation at 340 and 380 nm) is used, the resulting equation would be:
According to simple mathematics, c, d, and K can be canceled and the ratio can be described as:
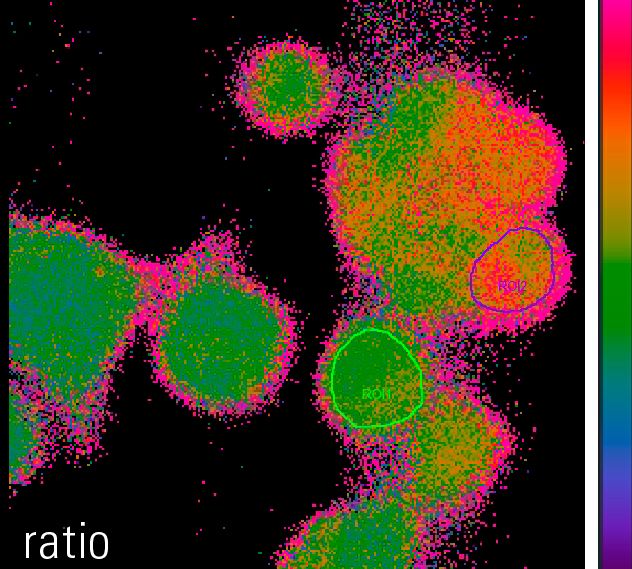
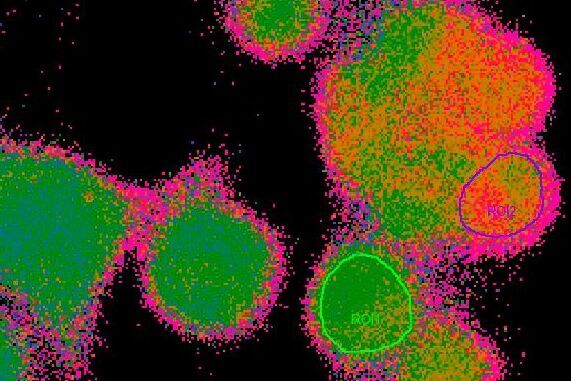
The virtual ratio image is calculated from two gray value images
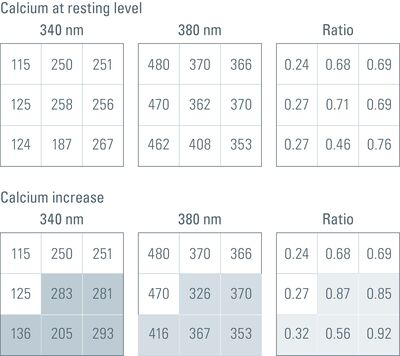
In practice, the ratio is calculated by a computer, in many cases online during a time-lapse experiment. By calculating the ratio of the gray values of corresponding pixels of two independently acquired gray value images, the ratio image is created. Remember that gray value images are basically a matrix of gray values with the size of the camera resolution or the region of interest (ROI) (usually 512x512, up to more than 1,000 x 1,000 pixels). In a calcium imaging time-lapse experiment with the dye Fura-2 (excitation: 340 nm and 380 nm, emission: 510 nm) this would work as follows (assuming that the images have the size 3 x 3 pixels):
This operation is performed for every pixel of every image pair in a time-lapse experiment, creating a ratio image stack. Finally, a false color map can be applied to the ratio image stack and the stack can then be watched and quantified like a normal gray value time-lapse movie.
Besides the advantages mentioned above, calculation of a ratio has an additional advantage. When performing live cell imaging with ion-, voltage- or pH-sensitive fluorophores, minute changes in fluorescence intensity at the respective wavelength often occur. In ratio imaging, however, an intensity increase at one wavelength and an intensity decrease at the other wavelength is observed in most cases (no matter whether the probe is excited or detected with two wavelengths). If the ratio of both acquired images is subsequently calculated, the difference between baseline and signal amplitude will be enhanced compared to the mere intensity change of the fluorophore. Hence, ratio imaging amplifies the amplitude of detected signals. This is of special interest for FRET assays, where the fluorescence intensity of the acceptor protein declines and the fluorescence intensity of the acceptor protein increases during the energy transfer.