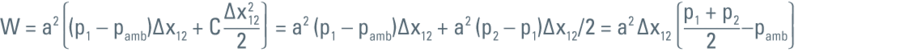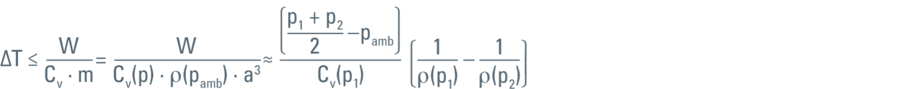Introducing high pressure will inevitably shift the parameters influencing the liquid phase in one direction or the other. The important question is whether the shift will be that significant to evoke a phase transition and if yes, is it going to be towards the solid or the liquid phase.
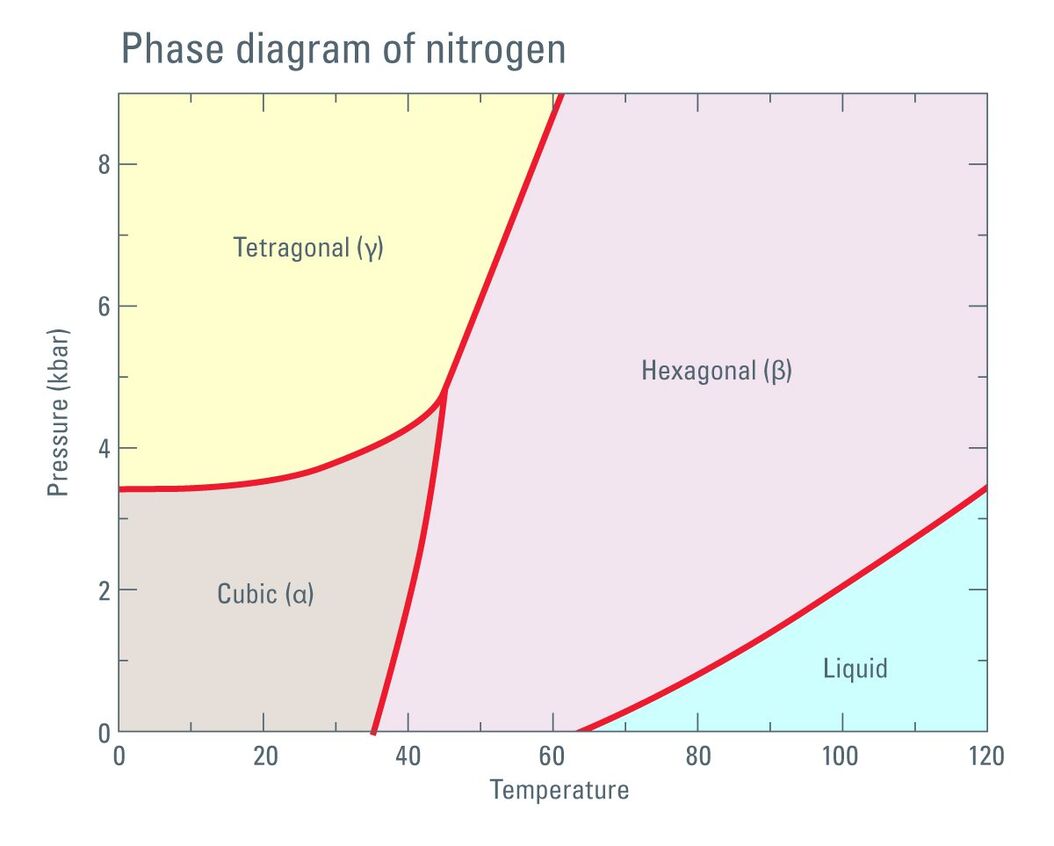
Fig. 1: Phase diagram of Nitrogen according to Young DA: Phase Diagrams of the Elements; UCRL-51902 (1975).
Compression and temperature shift of LN2
To create a pressurised LN2 jet we have to compress the liquid to a specific volume.
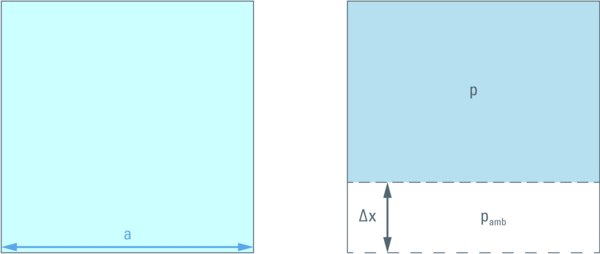
In order to illustrate this let us consider a cube with a given volume (a3) filled with liquid. One wall can be moved (by a distance ∆x ) in order to compress the liquid inside. This compression will create pressure difference between inside (p) and outside (pamb = 1,013 bar) the cube.
Compression is defined by the relative volume change in response to pressure change:
Where Δx12 is the shift of the wall necessary to compress the liquid from pressure p1 to pressure p2 and V(p1) is the volume of the liquid at p1.
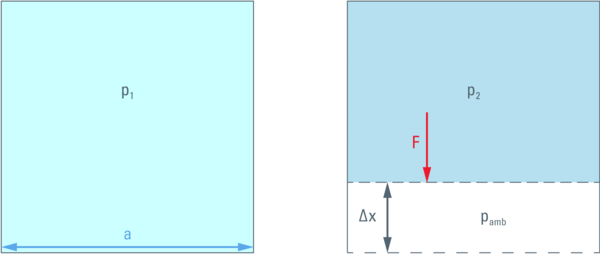
On the other hand, the pressure difference resulting from this compression, multiplied by the area of the side wall (a2) is the force (F) acting against the compression.
Therefore, a movement of the wall against this force by a distance Δx will require the energy F ⋅ Δx.
In order to compress the liquid from p1 to p2 the wall has to move through a certain distance and this move is the work (W) done to compress the liquid from p1 to p2.
For calculating the work (W) we use the following integral:
If we assume that the compression follows a linear compression law
Then the above integral can be evaluated as:
As energy is the capacity of a system to perform work, the work expressed in the formula above is then the energy that will eventually increase the temperature of the liquid (in this specific case the LN2):
where Cν represents the heat capacity and ρ(p) the density of LN2 at the pressure (p).
When this formula is applied to the data set given by Jacobsen et al. [1], it turns out that the work done for compression alone is not enough to warm LN2 above the freezing point.
In our calculations (performed for series of pressure sections for which the linear compression law is applicable) the direct compression of the liquid density would elevate the temperature to approximately 97 K. This means that at 200 MPa the work done (or the energy) would not be sufficient to keep the LN2 above the freezing point of 98.98 K.
Summary
Before we rush to any conclusions we have to consider a few other aspects. The temperature of 97 K is very close to the freezing point temperature, therefore we anticipate only 10 to 20 % of nitrogen to be frozen as the heat of fusion generated during the phase transformation will prevent further crystallisation. Additional heat which could probably increase the temperature above the freezing point is that heat generated by friction and the compression of gas bubbles. As these processes are very likely part of the system, they should be accounted for in the final estimation of the actual temperature of LN2.
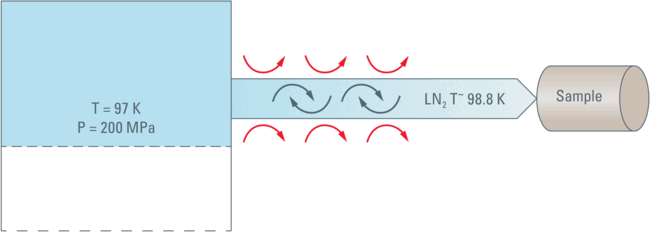
The calculations show that LN2 warms up during compression and is either a super-cooled liquid or a liquid with a small fraction of solid inclusions at 200 MPa.
If any such crystalline inclusions are actually formed they will surely "melt" when the Nitrogen is pushed towards the sample. The Nitrogen will be warmed by the contact with the tubing’s walls and by the occurrence of turbulence and friction during movement.
All this means that the nitrogen will reach the sample in its liquid form, most likely at a temperature in the range of –174.17 °C (or 98.98 K, the freezing point of LN2) or slightly higher.
Under the pressure of 200 MPa there is no Leidenfrost phenomenon thus the thermal contact with the sample cartridge is very good and the heat of the sample cartridge is, therefore, dissipated very efficiently by thermal conduction into the flowing LN2.